Warum ist statistische Signifikanz wichtig?
Erfahren Sie, warum statistische Signifikanz in der Datenanalyse, Forschung und bei Geschäftsentscheidungen eine Rolle spielt. Lernen Sie P-Werte, Hypothesentes...
Erfahren Sie, wie die statistische Signifikanz bestimmt, ob Ergebnisse echt oder zufällig sind. Verstehen Sie p-Werte, Hypothesentests und praktische Anwendungen für Ihr Unternehmen im Jahr 2025.
Statistische Signifikanz wird verwendet, um zu bestimmen, ob ein Ergebnis zufällig oder durch einen interessierenden Faktor verursacht wurde. Ist ein Ergebnis statistisch signifikant, ist es unwahrscheinlich, dass es zufällig aufgetreten ist.
Statistische Signifikanz ist ein grundlegendes Konzept in der Datenanalyse, das Ihnen hilft, zwischen echten Effekten und zufälligen Schwankungen in Ihren Daten zu unterscheiden. Wenn Sie Experimente durchführen, Umfragen auswerten oder Geschäftsmetriken analysieren, benötigen Sie eine zuverlässige Methode, um festzustellen, ob die beobachteten Muster tatsächlich existieren oder lediglich das Ergebnis von Zufall sind. Statistische Signifikanz bietet hierfür den entscheidenden Rahmen, indem sie mit mathematischen Prinzipien die Wahrscheinlichkeit bewertet, mit der Ihre beobachteten Ergebnisse eintreten würden, wenn tatsächlich kein Unterschied oder Effekt zwischen den verglichenen Gruppen besteht.
Das Konzept geht auf den Statistiker Ronald Fisher im frühen 20. Jahrhundert zurück und ist heute das Fundament des Hypothesentestens in nahezu allen datenbasierten Fachbereichen. Von der pharmazeutischen Forschung zur Validierung neuer Medikamente bis hin zu E-Commerce-Unternehmen, die Konversionsraten optimieren – statistische Signifikanz trennt handlungsrelevante Erkenntnisse von irreführenden Schlussfolgerungen. Wer versteht, wie statistische Signifikanz funktioniert, kann informierte Entscheidungen auf Basis von handfesten Belegen treffen, anstatt sich auf Intuition oder Zufall zu verlassen.
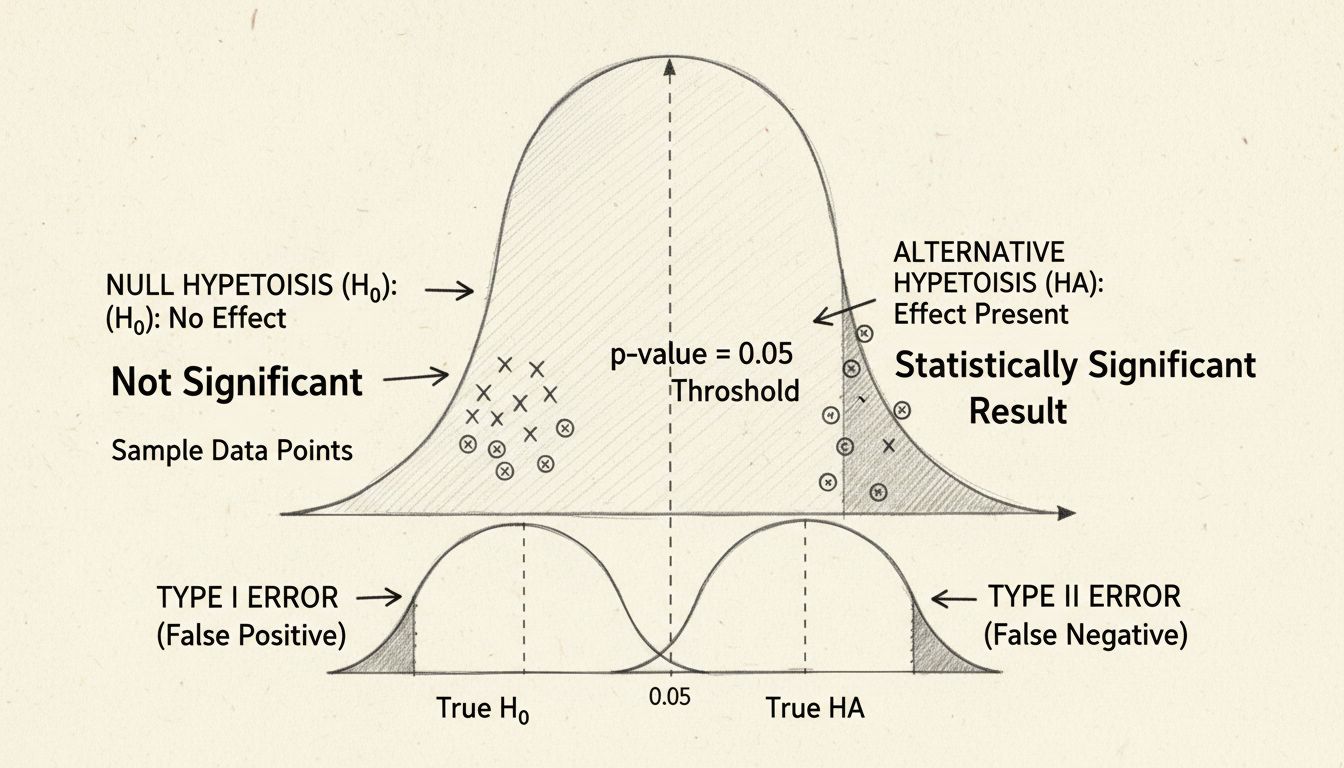
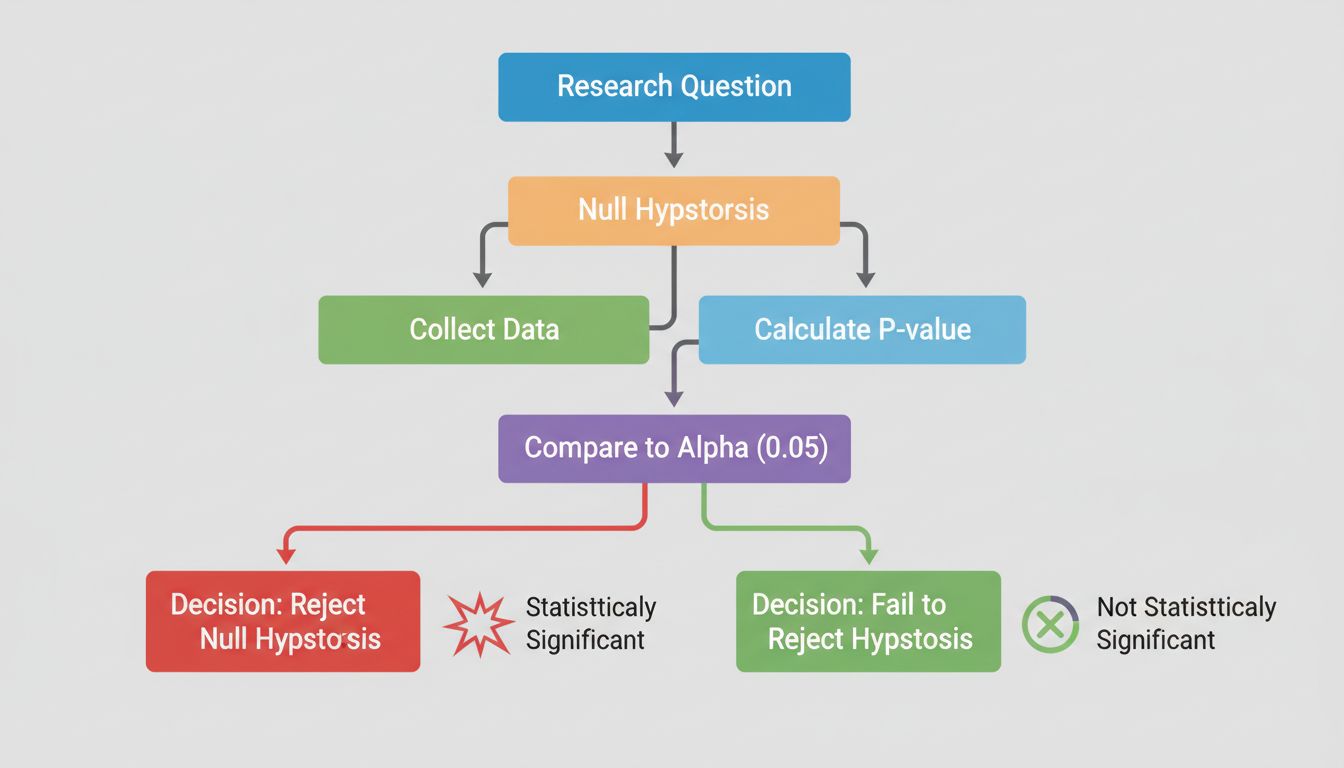
Im Zentrum der statistischen Signifikanz steht das Hypothesentesten – eine strukturierte Methode zur Bewertung von Behauptungen über Ihre Daten. Der Prozess beginnt mit der Formulierung zweier konkurrierender Hypothesen: der Nullhypothese und der Alternativhypothese. Die Nullhypothese geht davon aus, dass es keinen echten Effekt oder Unterschied zwischen den untersuchten Gruppen gibt – sie repräsentiert also den Status quo oder die Annahme, dass beobachtete Unterschiede rein zufällig sind. Die Alternativhypothese hingegen unterstellt, dass ein realer Effekt oder Unterschied existiert.
Ein praktisches Beispiel: Sie testen, ob eine neue Affiliate-Marketing-Kampagne höhere Konversionsraten erzielt als Ihre bisherige Strategie. Die Nullhypothese würde lauten, dass beide Kampagnen identische Konversionsraten liefern, während die Alternativhypothese einen Unterschied postuliert. Der statistische Test prüft, welche Hypothese von den Daten stärker gestützt wird. Dieses Vorgehen verhindert, dass Forscher oder Analysten nur die Ergebnisse auswählen, die ihre Erwartungen bestätigen – stattdessen müssen sie nachweisen, dass ihre Befunde mit hoher Wahrscheinlichkeit nicht zufällig sind.
Das Schöne am Hypothesentesten ist seine Objektivität. Statt auf subjektive Einschätzungen zu setzen, nutzen Sie mathematische Berechnungen, um zu bestimmen, ob Ihre Daten genug Belege bieten, um die Nullhypothese zu verwerfen. Ist das der Fall, können Sie mit Zuversicht behaupten, dass Ihr beobachteter Effekt statistisch signifikant ist – also nicht bloß ein Zufallsprodukt.
Der p-Wert ist vermutlich das am häufigsten verwendete Maß im Rahmen von Signifikanztests – und wird dennoch oft missverstanden. Der p-Wert repräsentiert die Wahrscheinlichkeit, Ihre Ergebnisse (oder noch extremere Resultate) zu beobachten, wenn die Nullhypothese tatsächlich wahr ist. Anders formuliert beantwortet er die Frage: „Wie wahrscheinlich ist es, dass ich diese Daten erhalte, wenn in Wirklichkeit kein Effekt existiert?“ Ein kleiner p-Wert bedeutet, dass Ihr Ergebnis unter der Nullhypothese sehr unwahrscheinlich wäre – was darauf hindeutet, dass die Nullhypothese wahrscheinlich falsch ist und Ihr Effekt real ist.
Der konventionelle Schwellenwert für statistische Signifikanz liegt bei einem p-Wert von 0,05 oder weniger, was einer 5%igen Wahrscheinlichkeit entspricht, dass das Ergebnis zufällig ist. Das heißt, Sie akzeptieren ein 5%-Risiko, die Nullhypothese fälschlicherweise zu verwerfen, obwohl sie stimmt (ein sogenannter Fehler 1. Art). Dieser Schwellenwert ist jedoch willkürlich und variiert je nach Fachbereich und Kontext. In der medizinischen Forschung, wo falsche Positivbefunde schwerwiegende Folgen haben können, wird oft ein strengerer Wert von 0,01 (1%) verwendet. Umgekehrt kann in explorativer Forschung ein Schwellenwert von 0,10 (10%) akzeptabel sein.
| P-Wert-Bereich | Interpretation | Typische Handlung |
|---|---|---|
| p < 0,01 | Hoch signifikant | Starke Evidenz gegen Nullhypothese |
| 0,01 ≤ p < 0,05 | Signifikant | Mäßige Evidenz gegen Nullhypothese |
| 0,05 ≤ p < 0,10 | Marginal signifikant | Schwache Evidenz gegen Nullhypothese |
| p ≥ 0,10 | Nicht signifikant | Nicht genügend Evidenz zum Verwerfen der Nullhypothese |
Es ist wichtig zu verstehen, was ein p-Wert nicht aussagt. Ein p-Wert von 0,03 bedeutet nicht, dass Ihre Hypothese mit 97% Wahrscheinlichkeit wahr ist. Er misst auch nicht die Größe oder praktische Bedeutung Ihres Effekts. Ein statistisch signifikantes Ergebnis kann immer noch einen trivial kleinen Effekt darstellen, der praktisch irrelevant ist. Die Unterscheidung zwischen statistischer und praktischer Signifikanz ist eine der häufigsten Fehlerquellen in der Datenanalyse.

Während p-Werte angeben, ob ein Effekt existiert, liefern Konfidenzintervalle entscheidende Informationen über die Größe und Genauigkeit dieses Effekts. Ein Konfidenzintervall ist ein Wertebereich, der mit einer bestimmten Wahrscheinlichkeit (typischerweise 95%) den wahren Effekt enthält. Prüfen Sie beispielsweise, ob ein neues Affiliate-Programm-Feature die Provisionen erhöht, könnte ein 95%-Konfidenzintervall anzeigen, dass die wahre Steigerung zwischen 2% und 8% liegt – mit 95%iger Sicherheit, dass der wahre Wert innerhalb dieses Bereichs liegt.
Konfidenzintervalle bieten im Vergleich zu reinen p-Werten mehrere Vorteile. Erstens zeigen sie Richtung und Stärke eines Effekts und liefern so ein vollständigeres Bild. Zweitens helfen sie, die praktische Relevanz einzuschätzen – ist ein Effekt statistisch signifikant, aber das Intervall zeigt einen verschwindend kleinen Effekt, lohnt sich die Umsetzung möglicherweise nicht. Drittens stehen enge Intervalle für präzise Schätzungen, während breite Intervalle auf Unsicherheit hinweisen.
Die Effektgröße misst die Stärke der Beziehung zwischen Variablen oder die Größe des Unterschieds zwischen Gruppen. Gängige Maße sind Cohen’s d (für Mittelwertvergleiche), Korrelationskoeffizienten und Odds Ratios. Ein Effekt kann statistisch signifikant sein, aber eine geringe Effektgröße haben – was bedeutet, dass der praktische Einfluss minimal ist. Umgekehrt kann eine große Effektgröße mangels ausreichender Stichprobe die Signifikanzschwelle verfehlen. Professionelle Analysten berichten immer Effektgrößen zusammen mit p-Werten, um ein vollständiges Bild zu vermitteln.
Die Stichprobengröße spielt eine entscheidende Rolle für die statistische Signifikanz. Größere Stichproben liefern mehr Informationen über die Grundgesamtheit und reduzieren den Einfluss zufälliger Schwankungen, wodurch echte Effekte leichter erkennbar sind. Kleine Stichproben hingegen sind anfälliger für Zufallsschwankungen und können sowohl zu falsch-positiven (Effekt wird fälschlicherweise festgestellt) als auch zu falsch-negativen Ergebnissen (Effekt wird übersehen) führen.
Der Zusammenhang zwischen Stichprobengröße und statistischer Power ist grundlegend für das Studiendesign. Statistische Power ist die Wahrscheinlichkeit, die Nullhypothese korrekt zurückzuweisen, wenn sie tatsächlich falsch ist – sprich, einen echten Effekt zu entdecken. Die meisten Forscher streben eine Power von 0,80 (80%) an, was bedeutet, dass sie bereit sind, einen 20%igen Fehler 2. Art (Übersehen eines Effekts) zu akzeptieren. Um diese Power zu erreichen, benötigen Sie eine ausreichend große Stichprobe – abhängig von erwarteter Effektgröße, gewähltem Signifikanzniveau und Testart.
Vor jeder Studie oder jedem Experiment sollte eine Power-Analyse durchgeführt werden, um die erforderliche Stichprobengröße zu bestimmen. So vermeiden Sie, dass Studien zu klein und damit ineffektiv oder überdimensioniert und damit ressourcenverschwendend ausfallen. Im Affiliate-Marketing bedeutet das: Sie sollten festlegen, wie viele Conversions oder Klicks benötigt werden, bevor Sie sicher beurteilen können, ob eine Kampagnenänderung tatsächlich wirkt.
Unterschiedliche Forschungsfragen und Datentypen erfordern verschiedene statistische Tests. Die Wahl hängt ab von der Anzahl der zu vergleichenden Gruppen, ob die Daten normalverteilt sind, ob es sich um unabhängige oder gepaarte Stichproben handelt und von der Art der Zielvariable (kontinuierlich, kategorisch usw.).
Der t-Test nach Student vergleicht die Mittelwerte zweier Gruppen und ist einer der am häufigsten eingesetzten Tests. Er eignet sich bei kontinuierlichen Daten (z.B. Umsatzbeträgen), wenn Sie wissen möchten, ob sich zwei Gruppen signifikant unterscheiden. Der Test berücksichtigt die Streuung innerhalb der Gruppen und die Stichprobengröße, um eine t-Statistik zu berechnen, die mit einem kritischen Wert verglichen wird.
Der Chi-Quadrat-Test wird für kategoriale Daten verwendet, um zu prüfen, ob beobachtete Häufigkeiten signifikant von erwarteten Häufigkeiten abweichen. Analysieren Sie beispielsweise, ob der Affiliate-Kanal (E-Mail, Social Media, Display-Anzeigen) die Konversionsrate beeinflusst, ist der Chi-Quadrat-Test passend.
ANOVA (Varianzanalyse) erweitert den t-Test auf den Vergleich von Mittelwerten über drei oder mehr Gruppen hinweg. Dies verhindert das Problem multipler Vergleiche, bei dem viele Einzeltests die Wahrscheinlichkeit von falsch-positiven Ergebnissen erhöhen.
Der Mann-Whitney-U-Test und der Wilcoxon-Rangsummentest sind nichtparametrische Alternativen, wenn die Voraussetzungen für parametrische Tests nicht erfüllt sind, etwa bei nicht normalverteilten Daten.
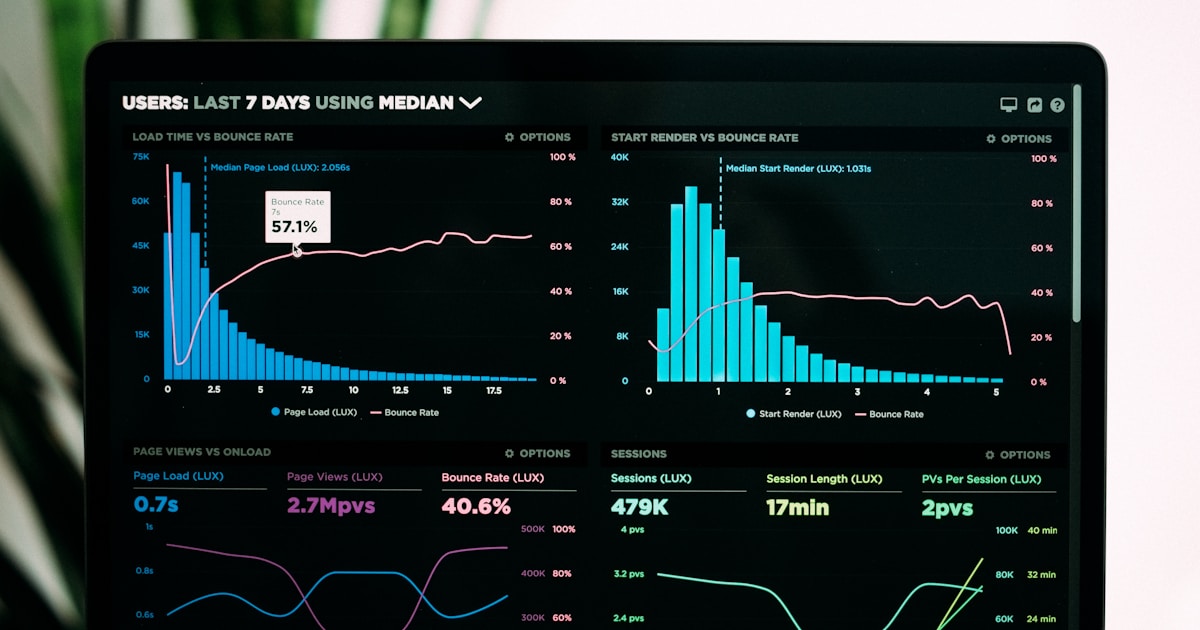
In der Geschäftswelt steuert statistische Signifikanz entscheidende Entscheidungen in zahlreichen Bereichen. Marketing-Teams nutzen A/B-Tests mit Signifikanzbewertung, um festzustellen, ob Website-Änderungen, E-Mail-Betreffzeilen oder Werbemittel die Performance tatsächlich verbessern. Anstatt sich auf Bauchgefühl oder Einzelbeobachtungen zu verlassen, legen datengetriebene Unternehmen Signifikanzschwellen vor Testbeginn fest und gewährleisten so, dass Entscheidungen auf belastbaren Belegen basieren.
Gerade im Affiliate-Marketing hilft Ihnen statistische Signifikanz, herauszufinden, welche Affiliates, Kampagnen und Werbestrategien wirklich Umsatz bringen – und welche nur scheinbar erfolgreich sind, weil der Zufall mitspielt. Wenn Sie etwa bewerten, ob eine neue Provisionsstruktur die Affiliate-Performance steigert, verhindern statistische Tests kostspielige Änderungen auf Basis kurzfristiger Schwankungen. Die Analytics-Plattform von PostAffiliatePro ermöglicht es Ihnen, Affiliate-Metriken mit der nötigen statistischen Präzision zu verfolgen, um fundierte Optimierungsentscheidungen zu treffen.
In der pharmazeutischen und medizinischen Forschung entscheidet die statistische Signifikanz darüber, ob neue Behandlungen wirksam genug sind, um Zulassung und Anwendung zu rechtfertigen. Klinische Studien müssen zeigen, dass der Nutzen eines Medikaments signifikant ist, bevor es verschrieben werden darf. Die Anforderungen sind hier besonders hoch, weshalb in der Medizin strengere Signifikanzniveaus üblich sind als in anderen Bereichen.
Eines der am weitesten verbreiteten Missverständnisse ist, dass statistische Signifikanz Kausalität beweist. Eine statistisch signifikante Korrelation zwischen zwei Variablen bedeutet nicht, dass eine die andere verursacht. Das klassische Beispiel ist die starke Korrelation zwischen Nicolas-Cage-Filmen und Ertrinkungsfällen – offensichtlich besteht kein kausaler Zusammenhang. Signifikanz zeigt lediglich an, dass eine Beziehung vermutlich nicht zufällig ist; Kausalität zu belegen, erfordert zusätzliche Evidenz wie einen logischen Mechanismus, zeitliche Abfolge und kontrollierte Experimente.
Ein weiterer häufiger Fehler ist das p-Hacking oder Data Dredging: Forscher führen zahlreiche Tests mit denselben Daten durch, bis sie signifikante Ergebnisse finden. Dadurch steigt die Wahrscheinlichkeit von falsch-positiven Resultaten, denn bei genügend vielen Tests wird zwangsläufig ein Ergebnis signifikant – rein zufällig. Führen Sie z. B. 20 unabhängige Tests mit einem Signifikanzniveau von 0,05 durch, ist statistisch gesehen ein falsch-positives Ergebnis zu erwarten. Verantwortungsbewusste Forscher legen Hypothesen und Testverfahren vor der Analyse fest und verhindern so dieses Problem.
Auch die Fehlinterpretation nicht signifikanter Ergebnisse ist ein Stolperstein. Ein nicht signifikantes Ergebnis beweist nicht, dass kein Effekt existiert; es bedeutet lediglich, dass keine ausreichende Evidenz zum Verwerfen der Nullhypothese vorliegt. Das kann an zu kleiner Stichprobe, hoher Datenstreuung oder tatsächlich ausbleibendem Effekt liegen. Fehlende Evidenz ist nicht gleichbedeutend mit Evidenz für das Fehlen eines Effekts.
Die Statistik entwickelt sich kontinuierlich weiter und viele Statistiker erkennen mittlerweile die Grenzen des traditionellen p-Wert-Ansatzes. Heute wird zunehmend empfohlen, p-Werte mit Effektgrößen, Konfidenzintervallen und Bayes’schen Methoden zu kombinieren. Die Bayes’sche Statistik, die Vorwissen einbezieht und Überzeugungen auf Basis beobachteter Daten aktualisiert, bietet ein alternatives Rahmenwerk, das manche Forscher als intuitiver und flexibler als klassische Ansätze empfinden.
Sequenzielle Tests und adaptive Designs gewinnen an Bedeutung. Sie erlauben es, Ergebnisse bereits während der Datensammlung zu überwachen und auf Basis von Zwischenanalysen zu entscheiden, ob Studien fortgesetzt, angepasst oder gestoppt werden. Gerade im Geschäftsumfeld, wo schnelle Entscheidungen gefragt sind, ist dies sehr wertvoll. Werkzeuge wie der Stats Engine von Statsig setzen sequenzielle Tests mit Kontrolle der Falschentdeckungsrate um und ermöglichen so schnellere und präzisere Entscheidungen während Experimenten.
Die Replikationskrise in der Wissenschaft hat zudem die Bedeutung korrekter Interpretation statistischer Signifikanz unterstrichen. Viele veröffentlichte Befunde lassen sich nicht wiederholen – nicht zuletzt, weil Forscher und Fachpublikationen zu stark auf p-Werte fokussiert und Effektgrößen oder praktische Relevanz vernachlässigt haben. Die Zukunft gehört daher mehr Transparenz, dem Pre-Registration von Studien und der Veröffentlichung aller Ergebnisse – unabhängig von ihrer Signifikanz.
Um statistische Signifikanz effektiv zu nutzen, legen Sie Signifikanzniveau und Stichprobengröße vor der Analyse fest. So vermeiden Sie Versuchungen, Schwellenwerte nachträglich an die Ergebnisse anzupassen. Berichten Sie immer Effektgrößen und Konfidenzintervalle zusätzlich zum p-Wert, damit Ihre Befunde vollständig bewertet werden können. Berücksichtigen Sie die praktische Relevanz Ihrer Resultate – ein statistisch signifikanter Effekt kann real, aber zu klein für praktische Anwendungen sein.
Seien Sie transparent hinsichtlich Ihrer Methodik, etwa beim Umgang mit fehlenden Werten, Ausreißern und multiplen Vergleichen. Haben Sie mehrere Tests durchgeführt, wenden Sie Korrekturen wie die Bonferroni-Korrektur an, damit das Gesamtniveau der Signifikanz gewahrt bleibt. Dokumentieren Sie Ihren Analyseprozess und stellen Sie, wo möglich, Ihre Daten und Ihren Code zur Verfügung, um Überprüfbarkeit und Replikation zu ermöglichen.
Denken Sie schließlich daran: Statistische Signifikanz ist ein Werkzeug, kein Selbstzweck. Sie unterstützt Sie dabei, bessere Entscheidungen zu treffen, indem sie den Einfluss des Zufalls verringert. Sie sollte jedoch immer mit Fachwissen, praktischen Erwägungen und unternehmerischem Urteilsvermögen kombiniert werden. Im Affiliate-Marketing hilft Ihnen statistische Signifikanz, wirklich wirksame Strategien zu erkennen – doch auch Faktoren wie Implementierungskosten, Affiliate-Zufriedenheit und langfristige Tragfähigkeit sollten in Ihre strategischen Entscheidungen einfließen.
Die fortschrittlichen Analyse- und Berichtswerkzeuge von PostAffiliatePro helfen Ihnen, die Performance Ihrer Affiliates mit statistischer Genauigkeit zu verfolgen. Verstehen Sie, welche Kampagnen wirklich Ergebnisse liefern, und optimieren Sie Ihr Affiliate-Programm auf Basis zuverlässiger Dateneinblicke.

Erfahren Sie, warum statistische Signifikanz in der Datenanalyse, Forschung und bei Geschäftsentscheidungen eine Rolle spielt. Lernen Sie P-Werte, Hypothesentes...
Statistische Signifikanz drückt die Zuverlässigkeit gemessener Daten aus und hilft Unternehmen, echte Effekte von Zufall zu unterscheiden und fundierte Entschei...
Beherrschen Sie die statistische Signifikanz bei A/B-Tests für Wett-Affiliate-Kampagnen.
Cookie-Zustimmung
Wir verwenden Cookies, um Ihr Surferlebnis zu verbessern und unseren Datenverkehr zu analysieren. See our privacy policy.